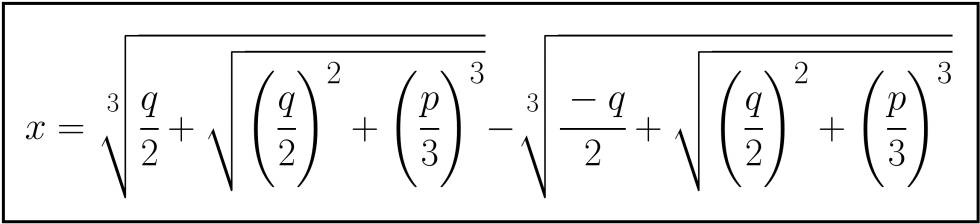LA HISTORIA DE LA ECUACION POLINÓMICA DE TECER GRADO
Nuestra historia se sitúa en el siglo XVI y tiene como protagonistas principales a Niccolo Fontana (Tartaglia) y Girolamo Cardano entre otros. En el siglo XVI llega a oídos de Tartaglia que un tal del Fiore posee un método para resolver ecuaciones cúbicas. En esa época poseer un método para resolver estas ecuaciones resultaba muy valioso. Por ello Tartaglia se puso a intentar encontrar ese método por sí mismo.
En aquella época, era habitual organizar desafíos entre matemáticos en los que cada uno proponía problemas que el otro tenía que resolver. Por ello Tartaglia desafío a del Fiore a un desafiío en el que ganó de manera aplastante.
Cuando Cardano tuvo conocimiento de esta aplastante victoria de Tartaglia, intenta convencerlo para que le revelara el método que había descubierto y así poder publicarlo en su obra Ars Magna. Aunque Tartaglia se negó en primera instancia, al final le reveló su descubrimiento con la condición de que no lo publicara.
Lo que Tartaglia había descubierto eran métodos para resolver las ecuaciones cúbicas que no tienen término de grado dos. Aunque en la actualidad todas ellas se reducen a una única forma, en aquella época se expresaban de estas tres maneras, x3+px=q, x3=px+q y x3+q=px, y cada una tenía su propio método de resolución . A partir de estos métodos, Cardano y su ayudante Ludovico Ferrari consiguen un método para resolver la cúbica general x3+mx2+nx=r. Esta ecuación puede reducirse fácilmente a una del tipo x3+px=q, por lo que solamente haría falta resolver ésta. Sus soluciones vienen dadas por la siguiente expresión: